当我们运行一个学习算法时,如果这个算法的表现不理想,那么有两种原因导致:要么偏差比较大、要么方差比较大。换句话说,要么是欠拟合、要么是过拟合。那么这两种情况,哪个和偏差有关、哪个和方差有关,或者是不是和两个都有关,搞清楚这点很重要。能判断出现的情况是这两种中的哪一种,是一个很有效的指示器,指引着可以改进算法的最有效的方法和途径。
下面深入地探讨一下有关偏差和方差的问题,并且能弄清楚怎样评价一个学习算法、能够判断一个算法是偏差还是方差有问题。因为这个问题对于弄清如何改进学习算法的效果非常重要。
如下图,用两个很简单的假设来拟合数据,比如说用一条直线,那么不足以拟合这组数据(欠拟合,左图),而如果你用两个很复杂的假设来拟合时,那么对训练集来说则会拟合得很好,但又过于完美(过拟合,右图)。而像这样的中等复杂度的假设(中间的图),比如某种二次多项式的假设,次数既不高也不低,这种假设对数据拟合得刚刚好。此时对应的的泛化误差,也是三种情况中最小的。
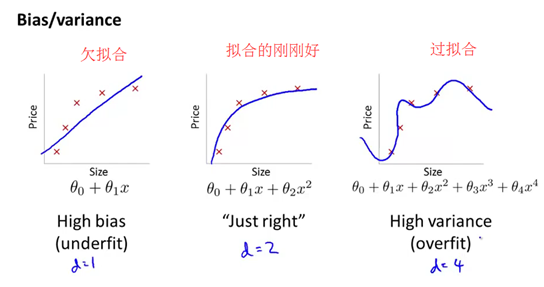
前面已经掌握了训练集、验证集和测试集的概念(),接下来就能更好地理解偏差和方差的问题。具体来说沿用之前所使用的训练集误差和验证集、误差的定义,也就是平方误差。即对训练集数据进行预测,或对验证集数据进行预测,所产生的平均平方误差。下面我们来画出如下这个示意图,横坐标上表示的是多项式的次数(中间图),因此横坐标越往右的位置,表示多项式的次数越大。那么我们来画这幅图对应的情况,d可能等于1的情况,是用很简单的函数来进行拟合。而在右边的这个图中,水平横坐标表示有更多更大的d值.表示更高次数的多项式。因此这些位置对应着使用更复杂的函数,来拟合训练集时所需要的d值。先画训练集误差,随着我们增大多项式的次数,我们将对训练集拟合得越来越好。所以如果d等于1时,对应着一个比较大的训练误差。而如果我们的多项式次数很高时,我们的训练误差就会很小,甚至可能等于0,因为可能非常拟合训练集。所以,当我们增大多项式次数时,不难发现训练误差明显下降(紫红色曲线)。这里写上J下标3来表示训练集误差。接下来再看交叉验证误差,如果我们观察测试集误差的话,我们会得到一个和交叉验证误差非常接近的结果。所以,我们知道如果d等于1的话,意味着用一个很简单的函数来拟合数据。也就是说,我们会得到一个较大的交叉验证误差(红色曲线标注1)。而如果我们用一个中等大小的多项式次数来拟合时,在前一张幻灯片中我们用的d等于2,那么我们会得到一个更小的交叉验证误差。因为我们找了一个能够更好拟合数据的次数。同样地,反过来,如果次数d太大,比如说d的值取为4,那么我们又过拟合了,我们又会得到一个较大的交叉验证误差。因此,如果你平稳地过渡这几个点,你可以绘制出一条平滑的曲线,就像这样,我用Jcv(θ)来表示(红色曲线)。同样地,如果你画出Jtest(θ),你也将得到一条类似的曲线,这样一幅图也同时能帮助我们更好地理解偏差和方差的概念。

具体来说,假设我们得出了一个学习算法,但这个算法并没有表现地如预期那么好。即交叉验证误差或者测试集误差都很大。那么我们应该如何判断此时的学习算法是高偏差的问题还是高方差的问题呢?交叉验证误差比较大的情况,对应着曲线中的左右两端(下图Jcv(θ)对应的曲线)。左端对应的就是高偏差的问题,也就是我们使用了一个过于小的多项式次数,比如d等于1。但实际上我们需要一个较高的多项式次数来拟合数据。相反地,右端对应的是高方差问题。也就是说,多项式次数d对于我们的数据来讲太大了。具体地说,第一、高偏差的情况,对应欠拟合的情况:交叉验证误差和训练误差都会很大。因此,如果你的算法有偏差问题的话,那么训练集误差将会比较大。同时你可能会发现交叉验证集误差也很大。两个误差可能很接近,或者可能验证误差稍大一点,所以如果你看到这样的组合情况,那就表示你的算法正处于高偏差的问题。第二、如果算法处于高方差的问题,那么Jtrain(训练误差)会很小。也就意味着,训练集数据拟合得非常好。而交叉验证集误差或者说交叉验证集对应的代价函数的值,将会远远大于训练集误差(双大于符号是一个数学符号,表示远远大于,用两个大于符号表示)。因此如果存在这种组合的情况,预示着学习算法可能正处于高方差和过拟合的情况。同时,区分这两种不同情形的关键依据是,如果算法处于高偏差的情况,那么你的训练集误差会很大。因为你的假设不能很好地拟合训练集数据。而当你处于高方差的问题时,你的训练误差通常都会很小,并且远远小于交叉验证误差。
